Solve the simultaneous equations 5x+2y=18 4x-2y=0

Question

asked Mar 8, 2019 107k views

2 Answers

Ibrar Ahmed · Answer 1 · 2019-03-09T21:29:07+0000

Since the order of equations makes us able to add al the like terms 5x + 4x; 2y + (- 2y); 18 + 0:

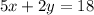
5x + 2y = 18

+

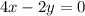
4x - 2y = 0

=

9x = 18

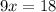
(We got that answer by summing the two equations. Note that 2y + (-2y) cancels out since it results in 0)

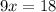9x = 18 → we take 9 to the right side of the equation

x = 18 / 9 → we solve for 18 / 9

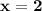$\bf~x = 2$ → final answer

Answer for x:

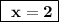
$\boxed{\bf~x=2}$

Now to solve for y we substitute all the x's by 2 in any of the equations you like, I'll choose the first one:

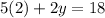5(2) + 2y = 18 → we solve for 5(2)

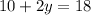10 + 2y = 18 → we take 10 to the right side of the equation

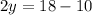2y = 18 - 10 → we solve for 18 - 10

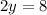2y = 8 → we take 2 to the right side of the equation

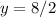y = 8 / 2 → we solve for 8 / 2

$\bf~y=4$ → final answer

Answer for y:

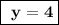
$\boxed{\bf~y = 4}$

Hope it helped,

BioTeacher101

(If you have any questions, feel free to ask them in the comments)