Answer:
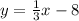
Explanation:
Slope-intercept form of an equation is written as
 , where
, where
 is the slope and
is the slope and
 is the y-intercept.
is the y-intercept.
The slope of a line that passes through the points
 and
and
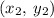 is
is
 . Using the coordinates
. Using the coordinates
 and
and
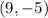 as given in the problem, we have slope of this line to be:
as given in the problem, we have slope of this line to be:
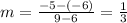 .
.
Now using this slope we've found and any point the line passes through, we can find the y-intercept of this equation:
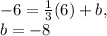
Therefore, the equation of this line in slope-intercept form is
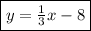 .
.