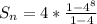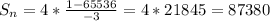Question

What is the sum of the geometric sequence 4, 16, 64, … if there are 8 terms?

21,845
43,690
65,535
87,380

Answer 1

`a_1=4,\ a_2=16,\ a_3=64\\\\\text{a ratio}\ r=(16)/(4)=4\\\\\text{The formula of a sum of the geometric sequence}\\\\S_n=a_1\cdot(1-r^n)/(1-r)\\\\\text{substitute}\\\\S_8=4\cdot(1-4^8)/(1-4)=4\cdot(1-65,536)/(-3)=4\cdot(-65,535)/(-3)=4\cdot21,845=\boxed{87,380}`

Answer 2

Sum is 87,380

Explanation:

the sum of the geometric sequence 4, 16, 64,...... 8 terms

To find the sum of geometric sequence use formula

`S_n = a_1 * (1-r^n)/(1-r)`

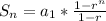
a_1 is the first term

r is the common ratio

To find out common ratio 'r', divide the second term by first term

16/4= 4

64/16= 4

r= 4

first term is also 4

plug in the values in the formula

`S_n = 4 * (1-4^8)/(1-4)`

`S_n = 4 * (1-65536)/(-3)=4*21845= 87380`