Question

In a community college parking lot, the number of ordinary cars is larger than the number of sport utility vehicles by 94.7%. The difference between the number of cars and the number of suvs is 18. Find the number of suvs in the lot.

Answer 1

The number of SUVs in the lot is 19.

Step-by-step explanation

Suppose, the number of SUVs in the lot is
`x`

As the number of ordinary cars is larger than the number of sport utility vehicles by 94.7% , so the number of ordinary cars will be:
`x+(x*0.947)=x+0.947x=1.947x`

Given that, the difference between the number of ordinary cars and the number of SUVs is 18. So the equation will be.....

`1.947x-x=18\\ \\ 0.947x=18\\ \\ x=(18)/(0.947)=19.0073... \approx 19`

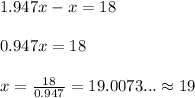
So, the number of SUVs in the lot is 19.