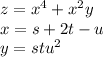
to proof - by using the chain rule.
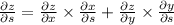
=
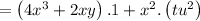
put the value of z, x and y.
we get
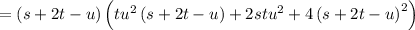
now put the value of s=4, t= 5, u=1 in the above question.
now by putting the value we get
= 14236
now we find the
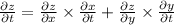
after doing differentiation
we get
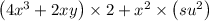
now the put the value of x,y,z
we get
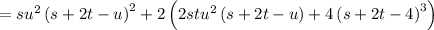
now we put the value of s=4, t=5,u=1
=19292
hence proved
now we find the value
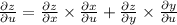
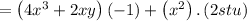
now put the value of x, y and z.
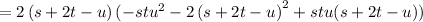
now put the value of u, v, z
we get
= -2548
hence proved