Answer : The half life of the radioisotope is 2.7 hours.
Explanation :
Radioactive disintegration is a first order reaction. The disintegration equation can be written as,
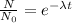
Here N is the amount of radioactive substance left = 8 counts
No is the initial amount of Radioactive substance = 64 counts
t is the time = 8 hours
λ is the disintegration constant
Let us rearrange the equation to solve for λ
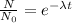
Take natural logarithm "ln" on both sides
![ln [(N)/(N_(0))]= - \lambda t](https://img.qammunity.org/2019/formulas/chemistry/high-school/5c407681kpwr4k3jqinkc7zbtqu2nxy0zp.png)
Divide both sides by t
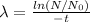
Let us plug in the given values.
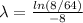
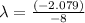

The disintegration constant, λ is 0.26.
λ and half life ( t1/2) are related to each other by following equation.
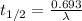
Let us plug in the value of λ
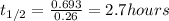
The half life of the radioisotope is 2.7 hours.