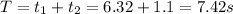Question

A model rocket blasts off and moves upward with an acceleration of 12 m/ss until it reaches a height of 29 m, at which point its engine shuts off and it continues its flight in free fall.

Answer 1

upward acceleration of rocket is given as

`a = 12 m/s^2`

`d = 29 m`

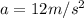
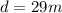
now the speed of rocket is given as

`v_f^2 - v_i^2 = 2 a d`

`v_f^2 - 0 = 2*12*29`

`v_f = 26.4 m/s`

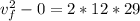
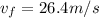
Here we can use kinematics again as after this the rocket starts free fall so its acceleration is a = 9.8 m/s^2

`v_f^2 - v_i^2 = 2 a d`

`0 - 26.4^2 = 2*(-9.8)*d`

`d = 35.5 m`

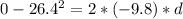
so the maximum height achieved by the rocket will be

`H = 35.5 + 29 = 64.51 m`

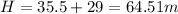
now the time of flight of rocket will be given as

first it will reach to height h = 29 m

`v_f - v_i = 2 a d`

`26.4 - 0 = 2*12 * t`

`t_1 = 1.1 s`

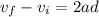
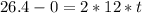
now after this it will move under free fall so time to reach the ground is given by

`d = v_i*t + (1)/(2) at^2`

`-29 = 26.4*t - (1)/(2)*9.8*t^2`

`4.9t^2 - 26.4 t - 29 = 0`

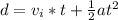
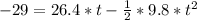
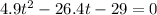
by solving above equation

`t = 6.32 s`

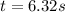
So total time of motion is

`T = t_1 + t_2 = 6.32 + 1.1 = 7.42 s`