According to Raoult's law:
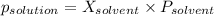 -(1)
-(1)
where
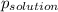 is observed vapor pressure of the solution,
is observed vapor pressure of the solution,
 is mole fraction of solvent, and
is mole fraction of solvent, and
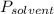 is vapor pressure of the pure solvent.
is vapor pressure of the pure solvent.
Vapor pressure of benzene =
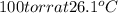 (given)
(given)
Reduction in vapor pressure on addition of non-volatile solute = 10.0 % (given)
So, vapor pressure of the component in the solution =
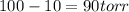
Substituting the values in formula (1):


Mole of benzene =
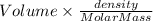
Mole of benzene =
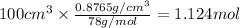
Since,
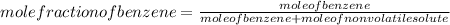
So,
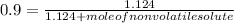
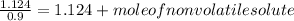
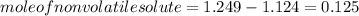
Hence, moles of a nonvolatile solute to be added is
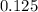 .
.