Question

Two spaceships approach the earth from opposite directions. According to an observer on the earth, ship a is moving at a speed of 0.753c and ship b at a speed of 0.851c. What is the velocity of ship a as observed from ship b

Answer 1

As per the question two spaceships A and B are approaching towards earth from opposite directions.

The velocity of ship A with respect to the observer on earth frame is 0.753c

where c is the velocity of light i.e 3×
`10^(8) m/s`

Hence
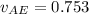`v_(AE) =0.753`c

Again the velocity of spaceship B with respect to the observer on earth frame is 0.851c i.e
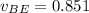`v_(BE) =0.851`c

Now we have to calculate the velocity of space ship A with respect to the space ship B.

We know
`v_(AB) =v_(AE) +v_(EB)`

=
`v_(AE) -v_(BE)` [
`v_(XY) = -v_(YX)`]

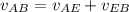
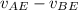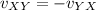=0.753c-0.851c

= -0.098c [ans]

Answer 2

`v_(AB)=0.977c`

Step-by-step explanation:

It is given that,

Speed of ship A,
`v_A=0.753c`

Speed of ship B,
`v_B=0.851c`

Let
`v_(AB)` is the velocity of ship A as observed from ship B. It can be calculated using the formula as :

`v_(AB)=(v_A+v_B)/(1+(v_Av_B)/(c^2))`

Substituting all the values in above formula as :

`v_(AB)=(0.753c+0.851c)/(1+(0.753c* 0.851c)/(c^2))`

`v_(AB)=0.977c`

So, the velocity of ship A as observed from ship B is 0.977c. Hence, this is the required solution.