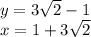If x2 + y2 = 38 and x - y = 2, then what is x? If there are two possible answers, then enter the larger of the two.

Question

asked Nov 8, 2019 92.5k views

2 Answers

TommasoF · Answer 1 · 2019-11-09T04:43:29+0000

Answer:

$y= 3√(2) -1 \\x = 1 +3√(2)\\$

Explanation:

First we can find x from the linear equation. So:

If x-y=2 then x=2+y

After that. We can inster x value in the cuadratic equation:

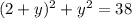
$(2 + y) {}^(2) + y {}^(2) = 38$

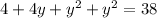
$4 + 4y + y {}^(2) + {y}^(2) = 38$

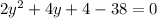
$2y {}^(2) + 4y + 4 - 38 = 0$

$2y {}^(2) + 4y -34 = 0$

After reorganizing terms and using factorization methods:

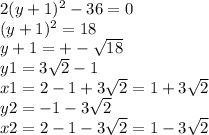
$2 (y+1)^2 - 36 = 0\\(y+1)^2 = 18\\y + 1 = +-√(18) \\y1 = 3√(2) -1 \\x1 = 2 -1 + 3√(2)=1 +3√(2)\\y2 = -1 - 3√(2)\\x2 = 2 -1 - 3√(2)=1 -3√(2)\\$

Finally we choose the largest value for x.

$y = 3√(2) -1 \\x = 1 +3√(2)\\$