Question

Let g' be the group of real matricies of the form [1 x 0 1]. Is the map that sends x to this matrix an isomorphism?

Answer 1

Yes. Conceptually, all the matrices in the group have the same structure, except for the variable component
`x`. So, each matrix is identified by its top-right coefficient, since the other three entries remain constant.

However, let's prove in a more formal way that

`\phi:\ \mathbb{R} \to G,\quad \phi(x) = \left[\begin{array}{cc}1&x\\0&1\end{array}\right]`

is an isomorphism.

First of all, it is injective: suppose
`x \\eq y`. Then, you trivially have
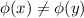`\phi(x) \\eq \phi(y)`, because they are two different matrices:

`\phi(x) = \left[\begin{array}{cc}1&x\\0&1\end{array}\right],\quad \phi(y) = \left[\begin{array}{cc}1&y\\0&1\end{array}\right]`

Secondly, it is trivially surjective: the matrix

`\phi(x) = \left[\begin{array}{cc}1&x\\0&1\end{array}\right]`

is clearly the image of the real number x.

Finally,
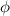`\phi` and its inverse are both homomorphisms: if we consider the usual product between matrices to be the operation for the group G and the real numbers to be an additive group, we have

`\phi (x+y) = \left[\begin{array}{cc}1&x+y\\0&1\end{array}\right] = \left[\begin{array}{cc}1&x\\0&1\end{array}\right] \cdot \left[\begin{array}{cc}1&y\\0&1\end{array}\right] = \phi(x) \cdot \phi(y)`