Question

Suppose the wavelength of the photon absorbed when nathan jumps from level 2 to 3 is 400 nm. What would be the wavelength of the photon nathan would have to absorb if he wanted to jump from levels 2 to 4

Answer 1

The wavelength of the photon nathan would have to absorb if he wanted to jump from levels 2 to 4 = 296.53 nm

Step-by-step explanation:

The energy of the absorbed photon can be found using,
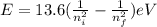`E = 13.6((1)/(n_i^2)-(1)/(n_f^2)) eV`, where
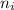`n_i` is the initial quantum level and
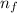`n_f` is the final quantum level.

And we also have E =hc/λ , where h is Planck's constant, c is the speed of light and λ is the wavelength of photon absorbed.

So E is inversely proportional to λ and E is directly proportional to
`((1)/(n_i^2)-(1)/(n_f^2))`

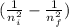
So λ is inversely proportional to
`((1)/(n_i^2)-(1)/(n_f^2))`

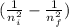
We have

`\lambda_1((1)/(2^2)-(1)/(3^2)) = \lambda_2((1)/(2^2)-(1)/(4^2)) \\ \\ 400*((1)/(2^2)-(1)/(3^2)) = \lambda_2((1)/(2^2)-(1)/(4^2))\\ \\ \lambda_2 = 400*0.139/0.1875 = 296.53nm`

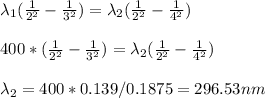
So the wavelength of the photon nathan would have to absorb if he wanted to jump from levels 2 to 4 = 296.53 nm