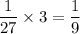Question

3 balls are placed in 3 boxes at random. What is the probability that exactly 2 boxes remain empty

Answer 1

If 2 boxes remain empty, it means that we put all three balls in one single box.

Suppose the full box is box number 1. For each ball, we have three choices - we may put it in box number 1, 2 or 3. This means that each box has a 1/3 chance of receiving each ball.

So:

• we choose box 1 for ball 1 - that's a 1/3 chance
• we choose box 1 for ball 2 - that's a 1/3 chance
• we choose box 1 for ball 3 - that's a 1/3 chance

So, the probability of putting all balls in box 1 is

`(1)/(3)*(1)/(3)*(1)/(3) = (1)/(3^3)`

But this is the probability of putting all ballx in box 1, and you can repeat this logic for box 2 and 3.

So, the probability of putting all balls in one single box is 1/27 for each box, for a total of

`(1)/(27) * 3 = (1)/(9)`