Step-by-step explanation:
It is given that,
Displacement,
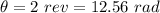
Initial angular velocity,
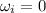
Final angular velocity,
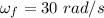
Let
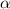 is its angular acceleration. Using the third equation of kinematics to find it as :
is its angular acceleration. Using the third equation of kinematics to find it as :
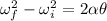
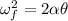
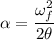
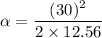
Angular acceleration,
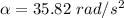
Let t is the time required to find it as :
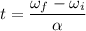
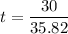
t = 0.83 seconds
So, the angular acceleration of the gear is
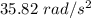 and the time taken is 0.83 seconds.
and the time taken is 0.83 seconds.