As per the question the charge of one coulomb is at 0 cm of the metre stick.the second charge of 4 coulomb is situated at at 100 cm of metre stick.
hence the separation distance between them is 100 cm.
now as per the question a proton is set up between them in such a way that the net force on it is zero
let the charge of proton is q coulomb let the proton is situated at distance of x cm from the charge 1 coulomb.hence it is situated at a distance of 100-x cm from the charge 4 coulomb.
the force exerted by 1 coulomb on proton is-
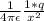
the force exerted by 4 coulomb on proton is-
![(1)/(4\pi\epsilon) (q*4)/([100-x]^2)](https://img.qammunity.org/2019/formulas/physics/high-school/w549jate8by86bvq9jygsi8xd4vfzvamrh.png)
as the net force is zero,hence-
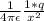
![=(1)/(4\pi\epsilon) (4*q)/([100-x]^2)](https://img.qammunity.org/2019/formulas/physics/high-school/vs4k6j9fl8bgwrfazg9mpos2yxvei0ywe0.png)
![=(1)/(x^2) =(4)/([100-x]^2)](https://img.qammunity.org/2019/formulas/physics/high-school/76c8m1cr5pvppt6fc168lgif7or7sy791o.png)
![x^2=([100-x[^2)/(4)[/tex</p><p>[tex]x=(100-x)/(2)](https://img.qammunity.org/2019/formulas/physics/high-school/83u1jcq7u7p76ev8it3pm4jnc7i54h740o.png)
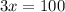
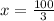
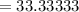 cm [ans]
cm [ans]