Question

The speed of a projectile when it reaches its maximum height is 0.58 times its speed when it is at half its maximum height. What is the initial projection angle of the projectile?

Answer 1

Speed of the projectile at its maximum height is only along horizontal direction

so at highest point

`v_1 = v_x`

now when he is at half of the maximum height the speed will be in x and y direction both

`v_2 = √(v_y^2 + v_x^2)`

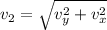
here it is given that

`v_1 = 0.58 v_2`

`v_x = 0.58√(v_x^2 + v_y^2)`

`2.97 v_x^2 = v_x^2 + v_y^2`

`1.97 v_x^2 = v_y^2`

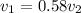
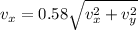
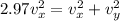
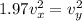
also we know that

`v_y^2 = v_(iy)^2 - 2 g (H)/(2)`

here we know that maximum height is given as

`H = (v_(iy)^2)/(2g)`

`v_y^2 = v_(iy)^2 - 2 g(v_(iy)^2)/(4g)`

`v_y^2 = (v_(iy)^2)/(2)`

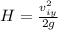
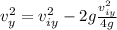
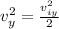
now from above

`1.97 v_x^2 = (v_(iy)^2)/(2)`

`1.98 v_x = v_(iy)`

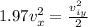
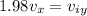
also we know that angle of projection is

`tan\theta = (v_(iy))/(v_x)`

`tan\theta = (1.98v_x)/(v_x)`

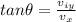
so angle is

`\theta = tan^(-1) 1.98`

`\theta = 63.3 degree`