Question

On the earth, an astronaut can safely jump to the ground from a height of 1.2 m ; her velocity when reaching the ground is slow enough to not cause injury. From what height could the astronaut safely jump to the ground on the moon?

Answer 1

We use the kinematic equation,

`v^(2) = u^(2) +2gh`

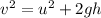
Here, u is initial velocity, and v is final velocity, g is acceleration due to gravity and h is maximum height.

The velocity of the astronaut reaching the ground from h is

`v=\sqrt{2 g_(earth) * h_(earth) }`

Here, u = 0.

Similarly, for moon

`v=\sqrt{2 g_(moon) * h_(moon) }`.

Take,
`g_(earth)  = 9.8 m/s^2` and
`g_(moon) = 1.625 \ m/s^2`.

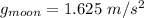For safe jump to the ground, the velocity should be same.

Therefore,

`\sqrt{2 g_(earth) * h_(earth) } = \sqrt{2 g_(moon) * h_(moon) } \\\\ </p><p>[tex]9.8  m/s^2 * 1.2 \ m = 1.625  m/s^2 * h_(moon) \\\\ h_(moon) = (11.76)/(1.625) = 7.2 \ m`

Thus, the astronaut safely jump to the ground on the moon from height 7.2 m.