Question

A spinning wheel is slowed down by a brake, giving it a constant angular acceleration of 25.60 rad/s2. During a 4.20-s time interval, the wheel rotates through 62.4 rad. What is the angular speed of the wheel at the end of the 4.20-s interval?

Answer 1

We use rotational kinematic equations,

`\theta =\theta _(0)  +  \omega_(0)  t+ (1)/(2)\alpha t^2` (A)

`\omega^2=  \omega^2_(0) +2\alpha\theta` (B)

Here,
`\theta` and
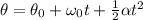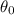`\theta _(0)` are final and initial angular displacements respectively,
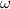`\omega` and
`\omega_(0)` are final and initial angular speed and
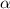`\alpha` is the angular acceleration.

Given,
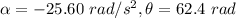`\alpha = - 25.60 \ rad/s^2, \theta = 62.4 \ rad` and
`t = 4 .20 \ s`.

Substituting these values in equation (A), we get

`62.4 \ rad = 0 +  \omega_(0)  4.20 \ s + (1)/(2) (- 25.60 \ rad/s^2) ( 4.20)^2 \\\\  \omega_(0) = (220.5+ 62.4 )/(4.20) =67.4 \ rad/s`

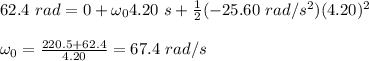
Now from equation (B),

`\omega^2=(67.4 \ rad/s)^2 + 2 (- 25.60 \ rad/s^2)62.4 \ rad \\\\\ \omega = 36.7 \ rad/s`

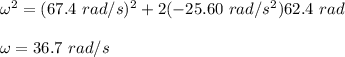
Thus, the angular speed of the wheel at the end of the 4.20-s interval is 36.7 rad/s.