Question

A rocket is shot straight up into the air with an initial velocity of 500 ft per second and from a height of 20 feet above the ground.

H=-16t^2+Vt+h

A) what is the height of the rocket 3 seconds after the launch?
B) at what time(s) is the rocket at a height of 400 feet above the ground?
C) how long will the rocket remain in the air?

Answer 1

The height of the rocket above the ground after
`t` seconds is given by the equation :
`H= -16t^2+Vt+h` , where
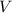`V` is the initial velocity and
`h` is the initial height.

Given that,
`V= 500 ft/second` and
`h= 20 ft`

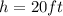
So, the equation will become:
`H= -16t^2 +500t+20`

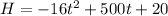
A) For finding the height of the rocket 3 seconds after the launch, we will plug
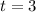`t=3` into the above equation. So....

`H= -16(3)^2+500(3)+20\\ \\ H= -16(9)+1500+20\\ \\ H= -144+1500+20=1376`

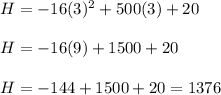
So, the height of the rocket 3 seconds after the launch is 1376 feet.

B) When the rocket at a height of 400 feet, then we will plug
`H= 400`

`400=-16t^2+500t+20\\ \\ 16t^2-500t-20+400=0\\ \\ 16t^2-500t+380=0\\ \\ 4(4t^2-125t+95)=0\\ \\ 4t^2-125t+95=0`

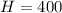
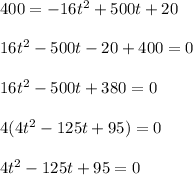
Using quadratic formula, we will get......

`t= (-(-125)+/-√((-125)^2-4(4)(95)))/(2(4))\\ \\ t= (125+/-√(14105))/(8)\\ \\ t= 30.4705... \\ and \\ t= 0.7794...`

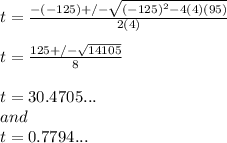
So, after 0.7794...seconds and 30.4705...seconds the rocket is at a height of 400 feet above the ground.

C) The time duration that the rocket remains in the air means we need to find the time taken by the rocket to reach the ground. When it reaches the ground, then
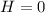`H=0`. So.....

`0=-16t^2+500t+20\\ \\ -4(4t^2-125t-5)=0\\ \\ 4t^2-125t-5=0`

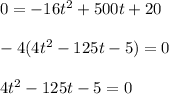
Using quadratic formula, we will get.....

`t= (-(-125)+/-√((-125)^2-4(4)(-5)))/(2(4))\\ \\ t= (125+/-√(15705))/(8)\\ \\ t=31.2899...\\ and\\ t= -0.0399...`

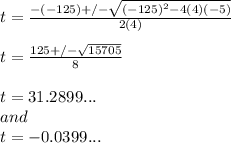
(Negative value is ignored as time can't be in negative)

So, the rocket will remain in the air for 31.2899... seconds.