For this, I will be factoring by grouping to solve for y.
Firstly, factor y^3 + 5y^2 and -9y - 45 separately, Make sure that they have the same quantity on the inside:
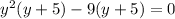
Now you can rewrite it as
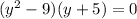 . However we are not finished factoring.
. However we are not finished factoring.
Now with y^2 - 9, we will apply the difference of squares rule, which is
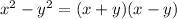 . Apply it as such:
. Apply it as such:
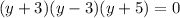
Now that it is completely factored, we can apply the Zero Product Property and solve for y:
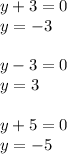
In short, y = -5, -3, and 3.