Question

Below are the range and standard deviation for a set of data. Use the range rule of thumb and compare it to the standard deviation listed below. Does the range rule of thumb produce an acceptable​ approximation? Suppose a researcher deems the approximation as acceptable if it has an error less than​ 15%. Range equals 2.76 standard deviation equals 0.807 the estimated standard deviation is nothing. ​(round to three decimal places as​ needed.) is this an acceptable​ approximation?

a. Yes​, because the error of the range rule of​ thumb's approximation is greater than​ 15%.
b. No​, because the error of the range rule of​ thumb's approximation is less than​ 15%.
c. Yes​, because the error of the range rule of​ thumb's approximation is less than​ 15%.
d. No​, because the error of the range rule of​ thumb's approximation is greater than​ 15%.

Answer 1

Solution: We are given:

`Range =2.76`

`Standard-deviation=0.807`

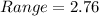
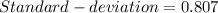
Now let's find the estimated value of standard deviation using the range rule of thumb. According to range rule of thumb, the estimate of standard deviation is:

`S\approx (2.76)/(4)= 0.690`

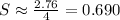
Therefore the estimated standard deviation is 0.690

is this an acceptable​ approximation?

Answer: c. Yes​, because the error of the range rule of​ thumb's approximation is less than​ 15%.

Step-by-step explanation:

The difference between estimated standard deviation and actual standard deviation is:

0.807 - 0.690 = 0.117

Now let's find the percentage of error

`(0.117)/(0.807) * 100= 14.50\%`.

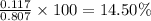Therefore, the error of the range rule of​ thumb's approximation is less than​ 15%.