We have been given gross domestic product (in billions of dollars) can be approximated by
 .
.
(a) In this part, we need to compute the derivative of this function:
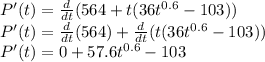
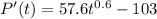
(b) In this part, we need to find the value of P'(45). So, we will substitute t=45
 Billion dollars per year.
Billion dollars per year.
(c) P'(45)=462.39 represents that 45 years after 1960, that is, in 2005, the GCP was changing at a rate of 462.39 billion dollars per year.