Question

Dr. Miriam johnson has been teaching accounting for over 20 years. From her experience, she knows that 60% of her students do homework regularly. Moreover, 95% of the students who do their homework regularly generally pass the course. She also knows that 85% of her students pass the course. Let event a be "do homework regularly" and b be "pass the course". Are the events "pass the course" and "do homework regularly" mutually exclusive?

Answer 1

Answer: The two events A "do homework regularly" and B "pass the course" are not mutually exclusive events since P(A and B) is 0.57, which is greater than 0.

As per the question,

Event A is : Do homework regularly

Event B is : Pass the course.

P(A) = 0.60

P(B) = 0.85

In probability the Probability of occurrence of events A or B is defined by two conditions:

If events A and B are mutually exclusive:

`P(A or B) = P(A) + P(B)` --- (1)

If events A and B are not mutually exclusive,

`P(A or B) = P(A) + P(B) - P(A and B)` ---- (2)

In other words, equations 1 and 2 will be equal only when P(A and B) =0.

Since 95% of the people who do homework regularly pass the course, we can derive the P(A and B) as

`P(A and B) = P(A) * P(B|A)`

`P(A and B) = 0.60 * 0.95`

`P(A and B) = 0.57`

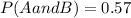
Since P(A and B) is greater than 0, the two events are not mutually exclusive.