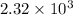Question

Determine the specific gravity of chlorine ​(cl 2​) gas at 21 degrees celsius​ [°c] and a pressure of 0.8 atmospheres​ [atm]. Assume chlorine is an ideal gas and obeys the ideal gas law. The molecular weight of chlorine is 70 grams per mole​ [g/mol].

Answer 1

Ideal gas law :

PV= nRT

where,

P = pressure

V= volume

n= number of moles

R= universal gas constant

T = temperature

Now, number of moles =
`(given mass in g)/(molar mass)`

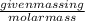
Put the value of number of moles in ideal gas law,

PV=
`(given mass in g)/(molar mass)`RT

PV=
`(m)/(M)`RT

PM=
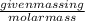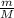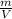`(m)/(V)`RT

Density is the ratio of mass to the volume, thus, above equation is also written as:

PM=
`\rho _(chlorine)`RT

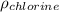`\rho _(chlorine)= (PM)/(RT)`

Put the values,

Temperature =
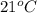`21^(o)C` + 273 =
`294 K`

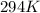
Pressure = 0.8 atm

`\rho _(chlorine)= (0.8 atm* 70 g/mol )/(0.082057 L atm mol^(-1)K^(-1)* 294^(o)C )`

=
`(56 atm g/mol )/(24.124758 L atm mol^(-1) )`

=
`2.32 g/L`

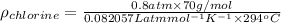
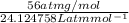
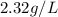
Now, specific gravity =
`(\rho _(chlorine))/(\rho _(water))`

=
`(2.32 g/L)/(1 g/cm^(3))`

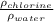
1 L = 1000
`cm^(3)`

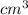
So, specific gravity =

`(2.32* 10^(3) g/cm^(3))/(1 g/cm^(3))`

=
`2.32 * 10^(3)`

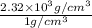
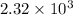
Thus, specific gravity is
`2.32 * 10^(3)`