Question

In a population distribution, a score of x=57 corresponds to z=-0.25 and a score of x=87 corresponds to z=1.25. Find the mean and standard deviation for the population.

Answer 1

Answer: The mean is 62 and the standard deviation is 20 for the population.

Explanation:

Let
`\mu` be the mean and
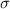`\sigma` be the standard deviation .

Formula to calculate z-score corresponds to random variable x on normal curve.

`Z=(X-\mu)/(\sigma),`

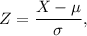
Given : In a population distribution, a score of x=57 corresponds to z=-0.25 and a score of x=87 corresponds to z=1.25.

`-0.25=(57-\mu)/(\sigma)\\\\-0.25\sigma=57-\mu---------(1)`

`1.25=(87-\mu)/(\sigma)\\\\1.25\sigma=87-\mu----------(2)`

Eliminate equation(1) from equation(2), we get

`1.50\sigma=30\\\\\Rightarrow\ \sigma=(30)/(1.5)=20`

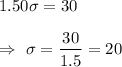
Put value of
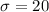`\sigma=20` in (1)

`1.25(20)=87-\mu\\\\87-\mu=25,\\\\\Rightarrow\mu=87-25=62.`

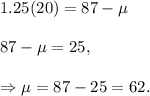
Hence, the mean is 62 and the standard deviation is 20 for the population.

Answer 2

Here is dependence between scores and x-values:

`Z_i=(X_i-\mu)/(\sigma),`

where
`\mu` is the mean,
`\sigma` is standard deviation and i changes from 1 to 2.

1. When i=1,
`Z_1=-0.25,\ X_1=57,` then

`-0.25=(57-\mu)/(\sigma).`

2. When i=2,
`Z_2=1.25,\ X_2=87,` then

`1.25=(87-\mu)/(\sigma).`

Now solve the system of equations:

`\left\{\begin{array}{l}-0.25=(57-\mu)/(\sigma)\\ \\1.25=(87-\mu)/(\sigma).\end{array}\right.`

`\left\{\begin{array}{l}-0.25\sigma=57-\mu\\ \\1.25\sigma=87-\mu.\end{array}\right.`

Subtract first equation from the second:

`1.25\sigma-(-0.25\sigma)=87-57,\\ \\1.5\sigma=30,\\ \\\sigma=20.`

Then

`1.25=(87-\mu)/(20),\\ \\87-\mu=25,\\ \\\mu=87-25=62.`

Answer: the mean is 62, the standard deviation is 20.