Question

You collect old coins. Today, you have two coins each of which is valued at $300. One coin is expected to increase in value by 6 percent annually while the other coin is expected to increase in value by 4.5 percent annually. What will be the difference in the value of the two coins 15 years from now

Answer 1

Present value of first coin = $300 and

Present value of second coin = $300.

First coin increasing rate = 6% annually = 6/100 = 0.06 times each year.

Second coin increasing rate = 4.5% annually = 4.5/100 = 0.045 times each year.

We know final value formula =
`Initial \ value*(1+ \ rate \ at \ which\ value \ increase)^(number \ of \ years)`.

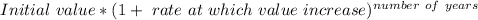Value of first coin after 15 years =
`300(1+0.06)^(15)` =
`300(1.06)^(15).`

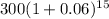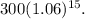
=300(2.39655819310) = 718.96745793

or 718.97 ( Upto two decimals).

Value of second coin after 15 years =
`300(1+0.045)^(15)=300(1.045)^(15)`.

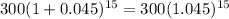= 300(1.93528244) = 580.584732927

or 580.58 (upto teo decimal places).

Diffrenece in the value of the two coins 15 years from now = 718.97 - 580.58.

= $138.39.

Therefore, the diffrenece in the value of the two coins 15 years from now is $138.39