Answer:
option A
Explanation:
A card is Chosen at random from a deck of 52 cards
there are 4 aces in the deck of 52 cards
Probability of picking a ace = total ace cards divide by total number of cards
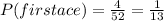
it is replaced and a second card is chosen
So total cards = 52 and ace =4
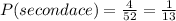
P(both are ace)=

=
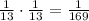
option A