The length of AC will be 2.5495.... cm.
Step-by-step explanation
In the diagram below, ABC is a right angle triangle with altitude as CD.
So, triangle ADC will be also a right angle triangle, in which CD = 2 cm.
In triangle ADC, using Pythagorean theorem we will get.....

Now in triangle ABC, using Pythagorean theorem.....
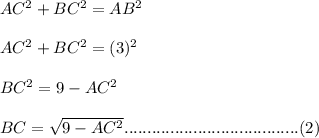
As it is given that AD = BC , so from equation (1) and (2) we will get.....
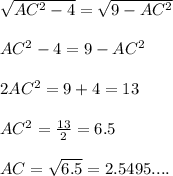
So, the length of AC will be 2.5495.... cm.