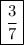Question

How do you simplify this expression?

Answer 1

Note that: (3/7)^5 = (3^5)/(7^5)

Also note that: (3^4/7^3)^2 = (3^8/7^6)

Divide

((3^5)/(7^5))/(3^8/7^6) = (3^5)/7^5) x (7^6)/(3^8) = 7/3^3 = 7/27

(9/7)^2 = 9/7 x 9/7 = 81/49

Multiply

81/49 * 7/27 = 567/1323 = 3/7

3/7 is your simplified answer

hope this helps

Answer 2

Solve the terms in parentheses first. We'll start on the denominator.

The denominator has an exponent for a fraction that also includes exponents. To multiply exponents within parentheses that are raised to a power, use this rule:

`(x^a)^b = x^(a \cdot b)`

Simplify the denominator:

`((3^4)/(7^3) )^2 = (3^8)/(7^6)`

Solve the fractions in the numerator:

`((3)/(5))^5 = (3^5)/(5^5)`

`((9)/(7))^2} = (9^2)/(7^2)`

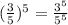
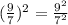
The problem should now read:

`((3^5)/(5^5) \cdot (9^2)/(7^2))/((3^8)/(7^6))`

There is a denominator in a denominator. We can bring that to the numerator of the overall fraction:

`((3^5)/(5^5) \cdot (9^2)/(7^2))/((3^8)/(7^6)) = \frac{(3^5)/(5^5) \cdot (9^2)/(7^2) \cdot {7^6}}{3^8}}`

Using a calculator, simplify the numerator:

`(3^5)/(5^5) \cdot (9^2)/(7^2) \cdot {7^6} = (19683)/(7)`

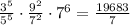
The fraction should now read:

`((19683)/(7))/(3^8)`

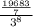
There is a denominator in the numerator. This can be brought down to the overall denominator:

`((19683)/(7))/(3^8) = (19683)/(3^8 \cdot 7)`

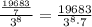
Factor 19683:

`19683 = 3 \cdot3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 = 3^9`

`(19683)/(3^8 \cdot 7) = (3^9)/(3^8 \cdot 7)`

Simplify the exponents:

`(3^9)/(3^8) = 3`

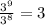
The following fraction will be your answer:

`\boxed{(3)/(7)}`