Question

How do I factor the difference of two squares

Answer 1

`\bf x^4-16\implies x^(2\cdot 2)-4^2\implies (x^2)^2-4^2\implies (x^2-4)(x^2+4) \\\\\\ (x^2-2^2)(x^2+4)\implies (x-2)(x+2)~~~~(x^2+4)`

Answer 2

Step-by-step explanation: If a variable is taken to an even power, that variable is a perfect square.

In this case,
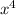`x^4` would therefore be a perfect square.

Since 16 is also a perfect square, what we

have here is the difference of two squares.

That can be factored as the product of two binomials,

one with a plus and one with a minus.

First ask yourself what are the factors of
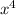`x^4` that are the same.

The rule is that those factors will use one-half

of the exponent on the original.

So the factors of
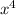`x^4` that are the same are
`x^2` and

We place these in the first position of each binomial.

The factors of 16 that are the same are 4 and 4.

So our answer is
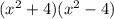`(x^2 + 4)(x^2 - 4)`.