Question

URGENT!!!! The area of a rectangular floor is 80 square feet. The length of the floor is 2 feet less than the width of the floor.

What is the width of the floor?

Drag the answers into the boxes to correctly complete the statements.


The equation Response area , where w is the width of the floor in feet, can be used to solve this problem. The width of the floor is Response area feet.

Answer 1

The width of the rectangular floor is 10 feet.

Step-by-step explanation:

The area of a rectangular floor can be found by multiplying the length and width of the floor. Let's call the width of the floor w. The length of the floor is 2 feet less than the width, so the length can be represented as w - 2. The equation for the area of the floor is w * (w - 2) = 80. To solve this equation, we can set it equal to zero and factor it: w^2 - 2w - 80 = 0.

Now we can solve the equation by factoring or using the quadratic formula. In this case, we can factor the equation as (w - 10)(w + 8) = 0. From this, we can see that the possible values for w are 10 and -8. However, since a negative width does not make sense in this context, the width of the floor is 10 feet.

Answer 2

Width of the floor = 10 feet

Step-by-step explanation:

Given that:

Area of rectangular floor = 80 square feet

Width of rectangular floor = w

Length of rectangular floor = w - 2

Now,

Area = Length * Width

80 = w(w-2)

`80=w^2-2w\\w^2-2w-80=0\\`

Factorizing the equation,

`w^2+8w-10w-80=0\\w(w+8)-10(w+10)=0\\(w+8)(w-10)=0`

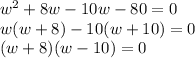
Either,

w+8 = 0

w = -8

Or,

w-10 = 0

w=10

As width cannot be negative,

width = 10 feet

Hence,

Width of the floor = 10 feet