Question

(2^8 x 3^−5 x 6^0)−2 x 3 to the power of negative 2 over 2 to the power of 3, whole to the power of 4 x 2^28

--

Answer 1

Here are a few rules about exponents:

1. Powering a power:
   `(x^m)^n=x^(m*n)`
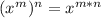
2. Zeroth power:
   `x^0=1`
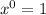
3. Multiplying exponents of the same base:
   `x^m*x^n=x^(m+n)`
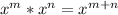
4. Dividing exponents of the same base:
   `(x^m)/(x^n)=x^(m-n)`

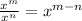
Firstly, cancel out the 6^0 and solve the power of powers:

`(2^8*3^(-5))^(-2)=2^(8*-2)3^(-5*-2)=2^(-16)3^(10)\\\\((3^(-2))/(2^3))^4=(3^(-2*4))/(2^(3*4))=(3^(-8))/(2^(12))\\\\2^(-16)3^(10)*(3^(-8))/(2^(12))*2^(28)`

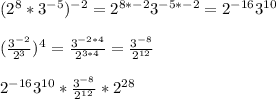
Next, multiply:

`(2^(-16)3^(10))/(1)*(3^(-8))/(2^(12))*(2^(28))/(1)=(2^(-16+28)3^(10+(-8)))/(2^(12))=(2^(12)3^(2))/(2^(12))`

Next, divide:

`(2^(12)3^(2))/(2^(12))=2^(12-12)3^(2-0)=2^03^2=3^2`

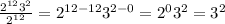
Your final answer is 3^2, or 9.

Answer 2

`(2^8\cdot3^(-5)\cdot6^0)^(-2)\cdot\left((3^(-2))/(2^3)\right)^4\cdot2^(28)\\\\=(2^8)^(-2)\cdot(3^(-5))^(-2)\cdot1^(-2)\cdot((3^(-2))^4)/((2^3)^4)\cdot2^(28)\\\\=2^(-16)\cdot3^(10)\cdot(3^(-8))/(2^(12))\cdot2^(28)\\\\=2^(-16)\cdot2^(28)\cdot2^(-12)\cdot3^(10)\cdot3^(-8)\\\\=2^(-16+28+(-12))\cdot3^(10+(-8))\\\\=2^0\cdot3^2=1\cdot9=\boxed{9}\\\\Used:\\\\(a\cdot b)^n=a^n\cdot b^n\\\\(a^n)^m=a^(n\cdot m)\\\\a^n\cdot a^m=a^(n+m)\\\\a^(-n)=(1)/(a^n)`