Answer: The required length of the longest side is 63 inches.
Step-by-step explanation: Given that the perimeter of the triangle shown is 162 inches.
We are to find the length of the longest side.
From the figure, we note that the lengths of the three sides of the triangle are 7x, 6x and 5x.
Since the perimeter of a triangle is equal to the sum of the lengths of the three sides, so we get
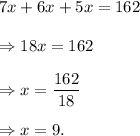
Therefore, the length of the longest side is given by
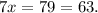
Thus, the required length of the longest side is 63 inches.