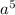1 Answer

Mohmmed Ali · Answer 1 · 2019-12-23T14:10:04+0000

We have been given the expression

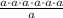
$(a\cdot a \cdot a \cdot a \cdot a \cdot a )/(a)$

We have to write this expression in the form
a^n

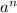
In order to write the given expression in this form, we can use some exponent property.

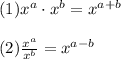
$(1) x^a\cdot x^b= x^(a+b)\\\\(2)(x^a)/(x^b)=x^(a-b)$

On using the property (1), we have

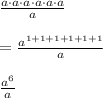
$(a\cdot a \cdot a \cdot a \cdot a \cdot a )/(a)\\\\=(a^(1+1+1+1+1+1))/(a)\\\\(a^6)/(a)$

Now, on using the property (2), we get

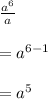
$(a^6)/(a)\\\\=a^(6-1)\\\\=a^5$

Therefore, the simplified form of the given expression is

a^5

Please log in or register to add a comment.