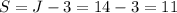2 Answers

Sheldon Griffin · Answer 1 · 2019-05-12T06:54:45+0000

Let J be the number of marbles owned by John, and S the number of marbles owned by Steve.

John has three more marbles than Steve, so
$J = S + 3 \iff J - S = 3$

They have 25 marbles, so
J+S = 25

So, we have the following system:

$\begin{cases} J - S = 3\\J + S = 25\end{cases}$

Add the two equations side by side:

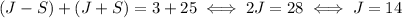
$(J - S) + (J + S) = 3 + 25 \iff 2J = 28 \iff J = 14$

Since John has three more marbles, we have

S = J - 3 = 14 - 3 = 11

Please log in or register to add a comment.