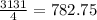Question

Of all rectangles with a perimeter of 3131​, which one has the maximum​ area? (give the​ dimensions.)

Answer 1

I'll tell you more: when you fix the perimeter of the rectangle, the one with the maximum area is always the square with that perimeter. Here's the proof.

Given a perimeter 2P, all rectangles with that perimeter have sides x and y such that

`2(x+y)=2P \iff x+y = P \iff x = P-y`

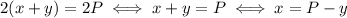
The area is the product of the dimensions, so

`A = xy = (P-y)y = -y^2+Py`

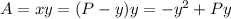
The maximum of this parabola is found by setting its derivative to zero:

`-2y + P = 0 \iff y = (P)/(2)`

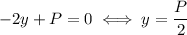
which implies

`x = P-y = P-(P)/(2) = (P)/(2)`

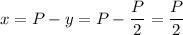
So, the maximum area is achieved when x=y, i.e. when the rectangle is actually a square.

So, the square with perimeter is 3131 has side length
`(3131)/(4) = 782.75`