Question

Colaco has a target of 16.00 ounces of liquid for each of their cans of soda. The current process is producing cans of soda with a mean of 15.97 ounces and a standard deviation of .04 ounces. What is the process capability if the upper tolerance limit is 16.1 and the lower tolerance limit is 15.9 ounces assuming a 99.7% quality level is required (+/- 3 standard deviations)? Is the process capable?

Answer 1

Solution: We are given:

`\mu=15.97,\sigma=0.04`

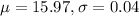
The process capability is

Upper tolerance limit is 16.1

Lower tolerance limit is 15.9

Now let's find the upper and lower limit of the given process assuming a 99.7% quality level is required (+/- 3 standard deviations):

`Lower-limit=\mu-3 \sigma`

`=15.97-3 * 0.4`

`=15.85`

`Upper-limit=\mu+3 \sigma`

`=15.97+3 * 0.4`

`=16.09`

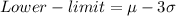
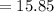
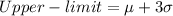
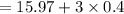
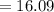
Since the lower and upper limits are beyond the given tolerance limits, therefore the is not capable.