Question

Calculate the radius of a vanadium atom, given that v has a bcc crystal structure, a density of 5.96 g/cm3 , and an atomic weight of 50.9 g/mol

Answer 1

`calculate the total number of unit cells in BCC structure\\</p><p>atoms=atoms at center+atoms at corners\\</p><p>atoms=1+(8*(1)/(8))\\</p><p>atoms= 2 atoms/unitcell\\</p><p>equate the length of the cube diagonal in terms of unit cell length,s and radius of atom R.\\</p><p>√(3s)=4R\\</p><p>s=(4)/(√(3))R\\</p><p>consider the volume of unit cell\\</p><p>v=s^3\\</p><p>=((4)/(√(3))R)\\</p><p>=(64)/(3√(3)R^3)\\</p><p>consider the density of vanadium atom\\</p><p>p=(nAv)/(Vn)\\`

Here, Avogadro’s number is N, number of atoms in unit cell is n, and atomic mass of the vanadium is , and volume of the unit cell is V.

`substitute (64)/(3√(3)R^3) for V.\\</p><p>6.022*10^23 atoms/mol for N,\\</p><p>2 for n 5.96g/km^3 for p.\\</p><p>and 50.9g/mol for the radius of the vanadium atom is 0.132nm.`

Answer 2

Answer: The radius of vanadium atom is 132.07 pm

Step-by-step explanation:

To calculate the edge length of metal, we use the equation:

`\rho=(Z* M)/(N_(A)* a^(3))`

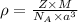
where,

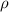`\rho` = density of metal =
`5.96g/cm^3`

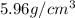
Z = number of atom in unit cell = 2 (BCC

M = atomic mass of metal = 50.9 g/mol

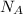`N_(A)` = Avogadro's number =
`6.022* 10^(23)`

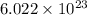
a = edge length of unit cell = ?

Putting values in above equation, we get:

`5.96g/cm^3=(2* 50.9)/(6.022* 10^(23)* (a)^3)\\\\a^3=2.836* 10^(-23)cm^3\\\\a=\sqrt[3]{2.836* 10^(-23)}=3.05* 10^(-8)cm^3=305pm`

To calculate the radius, we use the relation between the radius and edge length for BCC lattice:

`R=(√(3)a)/(4)`

where,

R = radius of the lattice = ?

a = edge length = 305 pm

Putting values in above equation, we get:

`R=(√(3)* 305)/(4)=132.07pm`

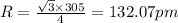
Hence, the radius of vanadium atom is 132.07 pm