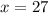Question

When the sum of \, 528 \, and three times a positive number is subtracted from the square of the number, the result is \, 120. Find the number?

Answer 1

Let
`x` be the unknown number. So, three times that number means
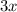`3x`, and the square of the number is
`x^2`

We have to sum 528 and three times the number, so we have
`528+3x`

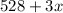
Then, we have to subtract this number from
`x^2`, so we have

`x^2-(3x+528)`

The result is 120, so the equation is

`x^2 - 3x - 528 = 120 \iff x^2 - 3x - 648 = 0`

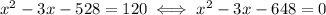
This is a quadratic equation, i.e. an equation like
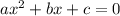`ax^2+bx+c=0`. These equation can be solved - assuming they have a solution - with the following formula

`x_(1,2) = (-b\pm√(b^2-4ac))/(2a)`

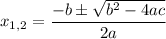
If you plug the values from your equation, you have

`x_(1,2) = (3\pm√(9-4\cdot(-648)))/(2) = (3\pm√(9+2592))/(2) = (3\pm√(2601))/(2) = (3\pm51)/(2)`

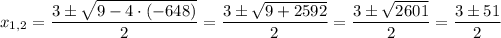
So, the two solutions would be

`x = (3+51)/(2) = (54)/(2) = 27`

`x = (3-51)/(2) = (-48)/(2) = -24`

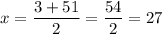
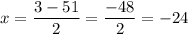
But we know that x is positive, so we only accept the solution
`x = 27`