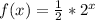Question

"write an equation in the form of f(x) = a*b^x with a base of 2" and passes through the point (4,4)

Answer 1

For this
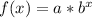`f(x) = a*b^x` equation, we can first identify the components.

f(x) is the output, or the y-coordinate.

a is the initial amount

b is the base

x is the input, or the x-coordinate.

Next, we can identify known variables.

We know for sure that the base is 2, since it is given in the problem.

We can also safely assume that since (4,4) is on the line, or the function, that it must be a solution of the equation.

Thus, (4,4) allows us to conclude that 4 is our x-coordinate and 4 is our y-coordinate.

Plug in known values.

`f(x) = a*b^x`

`(4) = a*2^4`

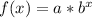
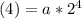
Simplify the problem.

`(4) = 8a`

Divide by 8 on both sides to get a alone.

`a = 1/2`

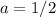
Plug in all values again, with the known value, and without the x and the f(x) value.

`f(x) = (1)/(2) *2^x`