Answer:
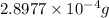 of mass is converted to energy.
of mass is converted to energy.
Step-by-step explanation:
Mass of 1 mole of carbon-11 = 11 g
Moles of carbon-11 in 1 gram :

Energy released when 1 mol of carbon-111 undergoes positron emission: E

Then energy released when 0.0909 moles of carbon-11 undergoes positron emission:
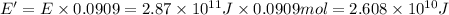
Let the mass converted into energy during the process be m
Using Einstein equation of energy:

E = energy released
m = mass converted into energy
c = speed of the light
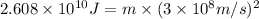
m =
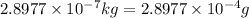
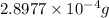 of mass is converted to energy.
of mass is converted to energy.