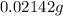The mathematical expression is given as:
 (1)
(1)
where,
 = depression in freezing point
= depression in freezing point
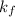 = molal freezing point.
= molal freezing point.
Now, first calculate the


Substitute the values in equation (1), we get

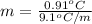
=
 or
or
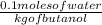
Now,
In 0.1 moles of water = 1 kg of butanol
So, 11.9 g of butanol =
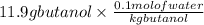
Convert gram into kilogram, (1 kg =1000 g)
=
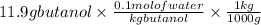
=
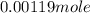
Mass of water present in sample =
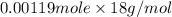
=
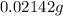
Hence, grams of water present in the sample =