Question

For altitudes up to 36,000 feet, the relationship between ground temperature and atmospheric temperature can be described by the formula t = −0.0035a + g, in which t is the atmospheric temperature in degrees Fahrenheit, a is the altitude, in feet, at which the atmospheric temperature is measured, and g is the ground temperature in degrees Fahrenheit. Solve the equation for a. If the atmospheric temperature is −25.4 

°

F and the ground temperature is 60 

°

F, what is the altitude?
 
The equation for a is a = 

.
 
If the atmospheric temperature is −25.4 

°

F and the ground temperature is 60 

°

F, then 
a = 

 feet.

Answer 1

Given formula : formula t = −0.0035a + g, where t is the atmospheric temperature in degrees Fahrenheit, a is the altitude in feet and g is the ground temperature in degrees Fahrenheit.

To find: 1) If the atmospheric temperature is −25.4 °F and the ground temperature is 60°F, what is the altitude?

2) The equation for a is a = .

Solution: 1) We have atmospheric temperature(t) =−25.4 °F, and

ground temperature(g) =60°F.

Plugging values of t and g in given formula t = −0.0035a + g, we get

-25.4 = −0.0035a + 60.

Subtracting 60 from both sides, we get

-25.4 - 60 = −0.0035a + 60-60

-85.4 = −0.0035a.

Dividing both sides by -0.0035, we get

-85.4/-0.0035 = −0.0035a/-0.0035.

24400 = a

Therefore, if the atmospheric temperature is −25.4 °F and the ground temperature is 60°F, the altitude is 24400 feet.

2) We need to solve equation for a in this part.

We have

t = −0.0035a + g

Subtracting g from both sides, we get

t -g = −0.0035a + g-g

t-g = −0.0035a

Dividing both sides by −0.0035, we get

(t-g)/-0.0035 = −0.0035a/-0.0035

`a=-(t-g)/(0.0035)`

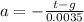
Distributing minus sign on the top, we get

`a=(g-t)/(0.0035)`.

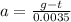Therefore, the equation for a is a =(g-t)/0.0035.