Let us assume first number is = x and second number is =y.
Adding those numbers we get 8. So we can setup first equation as
x+y=8. ..........................equation (1)
Multiplying those numbers we get -3. So we can setup second equation as
x*y=-3. ..........................equation(2).
we need to solve first equation for y
x+y=8 subtracting x from both sides, we get
x-x+y=8-x
y=8-x.
Substituting x=8-x in second equation, we get
x*(8-x)=-3.
Distributing x over (8-x), we get
8x -x^2 =-3
Adding 3 on both sides, we get
8x -x^2+3 =-3+3
-x^2 + 8x +3 = 0
We can solve this quadratic equation for x now.
We have a=-1, b=8 and c=3.
Plugging values of a, b and c in quadratic formula, we get

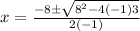
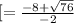 and
and
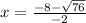
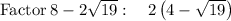
We get
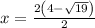 and
and
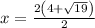
On simplfying above two values, we get
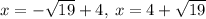
So, the required numbers are
 .
.