That's true.
In fact, suppose that x is irrational, and y is rational. If
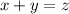
and z is rational, then you have
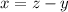
But
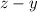 is the difference of two rational numbers, and the sum/difference of rational numbers is still a rational number.
is the difference of two rational numbers, and the sum/difference of rational numbers is still a rational number.
This proves that the sum of a rational and an irrational number is still irrational.