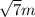Question

What is the height of an isosceles trapezoid, if the lengths of its bases are 5m and 11m, and the length of a leg 4m

Show your work plz :D

Answer 1

In the isosceles trapezoid ABCD, draw two perpendiculars AM and BL from A and B to the side CD.

Now, LM = BA = 5 m

CD = CL + LM + MD

= CL + 5 + CL (CL = MD)

= 2CL + 5

But, CD = 11

Therefore, 2CL + 5 = 11

2CL = 11 - 5

= 6

CL = 6/2 = 3m

MD = 3m

Now, consider the right triangle AMD.

We have,

`AM^(2) = AD^(2) - MD^(2)`

=
`4^(2) - 3^(2)`

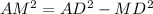
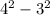
= 16 - 9

= 7

Hence, height of the isosceles trapezoid = AM =
`√(7) m`