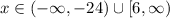Question

Please help ASAP!!
Algebra 2
Solve for x.

1/8x−5<−8 or 7x−4≥38

Answer 1

1/8x - 5 < - 8 7x - 4 > 38
+ 5 +5 +4 +4
1/8x < -3 7x > 42
÷1/8 ÷1/8 ÷7. ÷7
x = 24 x > 6

Answer 2

`x\in (-\infty,-24)\cup [6,\infty)`

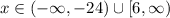
Explanation:

The given compound inequality is

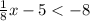`(1)/(8)x-5<-8` or
`7x-4\geq 38`

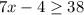
Solve each inequality.

On solving first inequality we get

`(1)/(8)x-5<-8`

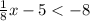
Add 5 on both sides.

`(1)/(8)x-5+5<-8+5`

`(1)/(8)x<-3`

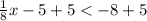
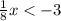
Multiply both sides by 8.

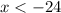`x<-24` .... (1)

On solving second inequality we get

`7x-4\geq 38`

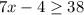
Add 4 on both sides.

`7x\geq 42`

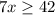
Divide both sides by 7.

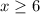`x\geq 6` .... (2)

Using (1) and (2) the value of x is either less than -24 or greater than or equal to 6.

`x\in(-\infty,-24)\cup [6,\infty)`