Refer to the attached image.
Given the rectangle ABCD of length 'l' and height 'h'.
Therefore, CD=AB = 'l' and BC = AD = 'h'
We have to determine the area of triangle AEF.
Area of triangle AEF = Area of rectangle ABCD - Area of triangle ADF - Area of triangle ECF - Area of triangle ABE
Area of triangle ADF =
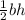
=
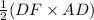
=

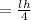
Area of triangle ECF =
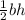
=
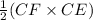
=

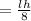
Area of triangle ABE =
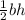
=
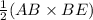
=

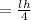
Now, area of triangle AEF =
Area of rectangle ABCD - Area of triangle ADF - Area of triangle ECF - Area of triangle ABE
=

=
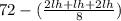
=
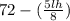
=

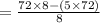
= 27 units
Therefore, the area of triangle AEF is 27 units.