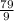Evaluate the infinite geometric series $0.79 + 0.079 + 0.0079 + 0.00079 + 0.000079 + \dotsb$. Express your answer as a fraction with integer numerator and denominator.

Question

asked Feb 14, 2019 163k views

2 Answers

Romain Rastel · Answer 1 · 2019-02-17T23:37:03+0000

Given geomatric series 0.79 + 0.079 + 0.0079 + 0.00079 + 0.000079 +.....

First term of the given geomatric series = 0.79.

Common ratio =
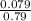(0.079 )/(0.79) =
(1)/(10)

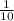
Sum of infinite geometric series is given by formula

S∞ =
(a)/(1-r)

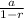
Where, a is the first term and r is the common ratio.

Plgging valus of a and r in above formula, we get

S∞ =
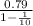
(0.79)/(1-(1)/(10) )

=
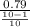
(0.79)/((10-1)/(10) )

=
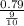
(0.79)/((9)/(10))

=
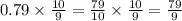
0.79*(10)/(9)=(79)/(10) *(10)/(9) = (79)/(9)

Therefore,

Sum of the infinite geometric series =
(79)/(9)