Question

The wave y1 = 0.12 sin π/3(5x+200t-1) propagates on a string of linear density 0.02 kg/m.

(a) Calculate the average power transmitted.

Answer 1

The average power transmitted by string wave is given by the expression
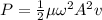`P=(1)/(2) \mu\omega^2A^2v`, Where μ is a linear density of a string, ω is angular frequency of the wave, A is an amplitude of the wave, v is a speed of wave.

Since
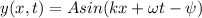`y(x,t)= A sin (kx+\omega t-\psi )` comparing with
`y_1 = 0.12 sin (\pi)/(3)(5x+200t-1)`

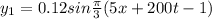
A = 0.12 m, ω =
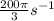`(200\pi )/(3) s^(-1)`, k =
`(5\pi )/(3) m^(-1)`

Speed of wave,
`v = (\omega )/(k) = ((200\pi )/(3))/((5\pi )/(3) ) =40m/s`

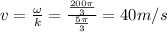
So power
`P = (1)/(2) *0.02*((200\pi )/(3) )^2*0.12^2*40=253 W`